编 者 的 话
教学是基础科学, 它是其他自然科学与工程技术的基础, 现代, 在社会科学某些领域里, 数学也浙渐受到重视.
数学的应用极其广泛, 它是工农业生产, 科学研究和工程技术的不可缺少的工具.
通常, 在学习和使用数学的过程中,往往需要寻找各种不同的关系和方法. 满足广大的大中学校师生、工程技术人员和一般的数学工作者的需要, 我们把一些常用的数学定理、公式、算法、解法、图象、数表以及其他有关的内容搜集成《数学手册》(以下简称《手册》), 供大家查阅.
编写本《手册》时力求内容全面. 《手册》包括初等数学、初等数论、微积分、解析几何与微分几何、高等代数、微分方程与积分方程、函数论、概率论、傅立叶分折、矢量与张量、特殊函数等一些常见的内容, 还包括某些广泛使用的数学方法,如最优化方法、有限元法、数理统计、实验数据处理等,同时对于那些通常认为比较抽象而又重要的数学理论, 如抽象代数、线性空间、一般拓扑学、泛函分析等也安排了一定的篇幅. 全书共二十一章.
参加编写本《手册》的有: 中国科学院数学研究所王连祥同志, 厦门大学数学系方德植、张鸣镛、林坚冰、辜联昆、锺同德、杨锡安、谢德平、骆镇华、肖必泉、蔡晖、林大兴等同志.
在编写《手册》的过程中,受到各方面同志的鼓励和帮助.王元、万哲先、陈兰荪、冯士雍、冯康、林群、顾基发、李文清、林鸿庆等同志对《手册》的部分内容多作了有益的修改.在此谨向这些同志致谢.
由于编者水平有限, 再加编写时间匆促, 所以一定存在不少缺点和错误, 恳切地希望读者批评和指正.
数 学 手 册
第一章 代数、三角公式与初等函数
这里收集和整理了初等代数(代数方程部分见第三章)、平面三角与球面三 角的一些常用公式,同时也介绍了-些常见的初等函数(一个实自变量)的简单 性质与图形,所以本章基本上包括了中等学校里的代数学和三角学的主要内容。
§1 代 数 公 式
一、数的扩张、分类及其基本运算规则
1. 数的扩张与分类表
\( \begin{aligned} &\text{自然数}\\ \text{(减法)}&\quad\downarrow \\ &\text{整 数} \begin{cases} \text{零}\\ \text{正整数(即自然数)}\\ \text{负整数} \end{cases}\\ \text{(除法)}&\quad\downarrow \\ &\begin{aligned} &\text{有理数}\\ &\text{(即分数)} \end{aligned}\left\{ \begin{aligned} &\text{零}\\ &\text{正有理数}\\ &\text{负有理数} \end{aligned} \right\} \begin{aligned} &\text{有限小数或}\\ &\text{无限循环小数} \end{aligned}\\ \text{(极限)}&\quad\downarrow \\ &\text{实 数} \begin{cases} \text{有理数}\\ \text{无理数}\left\{ \begin{aligned} \text{正无理数} \\ \text{负无理数} \end{aligned} \right\} \text{无限不循环小数} \end{cases}\\ \text{(代数方程)}&\quad\downarrow \\ &\text{复 数} \begin{cases} \text{代数数}\left( \begin{aligned} &\text{有理数、有理整数(即}\\ &\text{通常意义下的整数)和}\\ &\text{代数整数都是其特征} \end{aligned} \right)\\ \text{超越数(实超越数是无理数的特例)} \end{cases} \end{aligned} \)
2. 实数四则运算规则
[加减法规则] 同号两教相加,绝对值相加,符号与加数同;异号两数相加,绝对值相减(大的减小的),符号与绝对值大的加数同;任何实数和零相加,等于实数本身。减法是加法的逆运算,两个数相减只要把减数变成同它符号相反的数,即可按照加法规则运算。
[乘除法规则] 同号两数相乘,绝对值相乘, 符号位正;异号两数相乘,绝对值相乘,符号位负;任何数与零相乘等于零; 任何数与 1 相乘等于它自己,除法是乘法的逆运算, 同号两数相除, 绝对值相除;异号两数相除,绝对值相除, 符号为负; 任何数除以 1 等于它自己;零除以任何不等于零的数等于零;零不能做除数。
[四则混合运算规则] 先乘除,后加减;先括号内,后括号外。
3. 数的三个基本运算律
[交换律] \(\qquad a+b=b+a \qquad\qquad\qquad\quad ab=ba\)
[结合律] \(\qquad (a+b)+c=a+(b+c) \qquad abc=a(bc)\)
[交换律] \(\qquad (a+b)c=ac+bc\)
4. 乘方与开方
[乘方] n 个数 a 相乘
\begin{matrix}\underbrace{a\times a\times\cdots\times a=a^n} \\ n 个 \end{matrix}
称为 a 的 n 次(乘)方,又称为 a 的 n 次幂,α 称为幂底数,n称为幂指数.
从乘法的符号规则直接得出乘方的符号规则: 正数的任何次方为正数; 负数的偶次方为正数; 负数的奇次方为负数; 零的任何次方为零.
规定不等于零的数的零次方等于 1,即 \(a^0=1, a\ne0\).
[开平方] 若 \(a^2 = b\), 则 a 称为 b 的平方根, 记为\( a = \pm \sqrt{b} \), 求平方根的运算称为开平方,开平方的一般方法用下面例子说明.
例 求 316.4841 的平方根
解 第一步,先将被开方的数,从小数点位置向左右每隔两位用逗号 "," 分段,如把数 316.4841 分段成 3,16.48,41. 第二步,找出第一段数字的初商,使初商的平方不超过第一段数字,而初商加 1 的平方则大于第一段数字,本例中第一段数字为 3,初商为 1,因为 \(1^2=1<3\), 而 \((1+1)^2=4>3\). 第三步,用第一段数字减去初商的平方,并移下第二段数字,组成第一余数,在本例中第一余数为 216. 第四步,找出试商,使(20 x 初商 + 试商) x 试商不超过第一余数,而[20 x 初商 + (试商 + 1)] x (试商 + 1) 则大于第一余数. 第五步,把第一余数减去(20 x 初商 + 试商) x 试商, 并移下第三段数字,组成第二余数,本例中试商为 7,第二余数为 2748,依此法继续做下去,知道移完所有的段数,若最后余数为零,则开方运算告结束. 若余数永远不为零,则只能取某一精度的近似值. 第六步,定小数位点位置,平方根小数点位置应与被开放数的小数点位置对齐,本例的算式如下:
[开立方] 若\(a^3 = b\),则a称为b的立方根,记为\(a=\sqrt[3]{b}\),求立方根的运算称为开立方.
一个数的平方根和立方根可从“平方根表”和“立方根表”中查到.
5.实数进位制
[进位制的基与数字] 任一正数可表为通常意义下的有限小数或无限小数,各数字的值与数字所在的位置有关,任何位置的数字当小数点向右移一位时其值扩大10倍,当小数点向左移一位时其值缩小10倍.例如
\(173.246=1 \times 10^{2}+7 \times 10+3+2 \times 10^{-1}+4 \times 10^{-2}+6 \times 10^{-3}\)
一般地,任一正数a可表为
$$ \begin{aligned} a=& a_{n} a_{n-1} \cdots a_{1} a_{0} a_{-1} a_{-2} \cdots \\ =& a_{n} \times 10^{n}+a_{n-1} \times 10^{n-1}+\cdots+a_{1} \times 10+a_{0} \\ &+a_{-1} \times 10^{-1}+a_{-2} \times 10^{-2}+\cdots \end{aligned} $$
这就是10进数,记作\(a_{(10)}\),数10称为进位制的基,式中\(a_{i}\)在{0,1,2,...,9}中取值,称为10进数的数字,显然没有理由说进位制的基不可以取其他的数.现在取q为任意大于1的正整数当作进位制的基,于是就得到q进数表示
\(a_{(q)}=a_{n} a_{n-1} \cdots a_{1} a_{0} a_{-1} a_{-2} \cdots=a_{n} q^{n}+a_{n-1} q^{n-1}+\cdots+a_{1} q+a_{0}+a_{-1} q^{-1}+a_{-2} q^{-2}+\cdots\)
式中数字\(a_{i}\)在{0,1,2,...,q-1}中取值,\(a_{n} a_{n-1} \cdots a_{1} a_{0}\)称为q进数\(a_{(q)}\)的整数部分,记作[\(a_{(q)}\)];
\(a_{-1} a_{-2} \cdots\)称为\(a_{(q)}\)的分数部分,记作{\(a_{(q)}\)}.常用进位制,除10进制外,还有2进制、8进制、16进制等,其数字如下
$$ \begin{aligned} 2 \text { 进制 }\qquad & 0,1 \\ 8 \text { 进制 }\qquad & 0,1,2,3,4,5,6,7 \\ 16 \text { 进制 }\qquad & 0,1,2,3,4,5,6,7,8,9 \\ & \overline{0}, \overline{1}, \overline{2}, \overline{3}, \overline{4}, \overline{5} \end{aligned} $$
[2,8,16进制的加法与乘法表]
[8-2,16-2数字转换表]
[各种进位制的相互转换]
1° q->10转换 适用通常的10进数四则运算规则,根据公式(1),可以把q进数\(a_{(q)}\)转换为10进数表示.例如
$$ 743_{(8)}=7 \times 8^{2}+4 \times 8+3=448+32+3=483_{(10)} $$
$$ \begin{aligned} 1011.101_{(2)} &=1 \times 2^{3}+0 \times 2^{2}+1 \times 2+1+1 \times 2^{-1}+0 \times 2^{-2}+1 \times 2^{-3} \\ &=11.625_{(10)} \end{aligned} $$
2° 10->q转换 转换时必须分为整数部分和分数部分进行.
对于整数部分其步骤是:
(1)用q去除[\(a_{(10)}\)],得到商和余数.
(2)记下余数作为q进数的最后一个数字.
(3)用商替换[\(a_{(10)}\)]的位置重复(1)和(2)两步,直到商等于零为止.
对于分数部分其步骤是:
(1)用q去乘{\(a_{(10)}\)}.
(2)记下乘积的整数部分作为q进数的分数部分的第一个数字.
(3)用乘积的分数部分替换{\(a_{(10)}\)}的位置,重复(1)和(2)两步,直到乘积变为整数为止,或直到所需要的位数为止.例如:
$$ 103.118_{(10)}=147.074324 \cdots_{(8)} $$
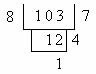
3° p->q转换 通常情况下其步骤是:\(a_{(p)} \rightarrow a_{(10)} \rightarrow a_{(q)}\).如果p,q是同一数s的不同次幂,其步骤是:\(a_{(p)} \rightarrow a_{(s)} \rightarrow a_{(q)}\).例如,8进数\(127.653_{(8)}\)转换为16进数时,由于8=23,16=24,所以s=2,其步骤是:首先把8进数的每个数字根据8-2转换表转换为2进数(三位一组)
$$ 127.653_{(8)}=001 \ 010 \ 111.110 \ 101 \ 011_{(2)} $$
然后把2进数的所有数字从小数点起(左和右)每四位一组分组,从16-2转换表中逐个记下对应的16进数的数字,即
$$ 127.653_{(8)}=0101 \ 0111.1101 \ 0101 \ 1000_{(2)}=57 . \overline{3} 58_{(10)} $$
二、复数
1.复数的概念
[实部与虚部·模与辐角·共轭复数] 复数\(z\)一般表示为\(z=a+ib\),其中\(i=\sqrt{-1}\)称为虚数单位,a和b均为实数,分别称为z的实部和虚部,记为\(a=\operatorname{Re} z\),\(b=\operatorname{Im} z\).
两个复数只有当实部和虚部分别相等时才相等.
\(|z|=\sqrt{a^{2}+b^{2}}\) 称为复数z的模.
\(\operatorname{Arg} z=\operatorname{Arc tg} \frac{b}{a}\)称为复数z的辐角,所以,一个复数有无穷多个辐角,但其中一个叫做主辐角,记为\(\operatorname{arg} z\),它满足
\(0\leq arg z < 2π\)
并有 \(\operatorname{Arg} z=\operatorname{arg} z+2kπ \qquad (k=0,±1,±2,...)\)
\(z=a+ib\) 与 \(\overline{z}=a-ib\)
[虚数单位的乘方]
2.复数的表示法
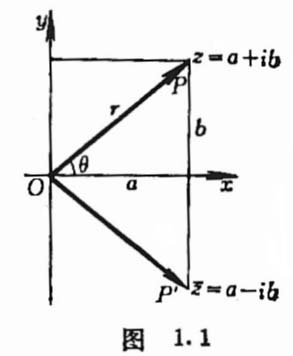
[坐标表示法] 复数\(z=a+ib\)可与直角坐标(a,b)建立一一对应(图1.1).
[矢量表示法] 把a,b视为矢量\(\overrightarrow{O P}\)在x轴和y轴上的投影,则矢量\(\overrightarrow{O P}\)(图1.1)可表示复数\(z=a+ib\),与\(P\)点关于x轴对称的点记为\(P'\),矢量\(\overrightarrow{O P'}\)表示共轭复数\(\overline{z}=a-ib\).
[三角表示法] $$ \begin{aligned} &z=|z|(\cos \theta+i \sin \theta) \\ &=r(\cos \theta+i \sin \theta) \end{aligned} $$
[指数表示法] \(z=|z| e^{i \theta}=r e^{i \theta}\)
3.复数的运算
[代数式运算]
\((a+ib) \pm (c+id)=(a \pm c)+i(b \pm d)\)
\((a+ib) \times (c+id)=(ac - bd)+i(bc + ad)\)
\((a+i b) \div(c+i d)=\frac{a c+b d}{c^{2}+d^{2}}+i \frac{b c-a d}{c^{2}+d^{2}}\)
[三角式运算] 设 $$ z_{1}=r_{1}\left(\cos \theta_{1}+i \sin \theta_{1}\right) \quad z_{2}=r_{2}\left(\cos \theta_{2}+i \sin \theta_{2}\right) $$
则
$$ z_{1} \cdot z_{2}=r_{1} r_{2}\left[\cos \left(\theta_{1}+\theta_{2}\right)+i \sin \left(\theta_{1}+\theta_{2}\right)\right] $$
$$ \frac{z_{1}}{z_{2}}=\frac{r_{1}}{r_{2}}\left[\cos \left(\theta_{1}-\theta_{2}\right)+i \sin \left(\theta_{1}-\theta_{2}\right)\right] $$
$$ z_{1}^{n}=r_{1}^{n}\left(\cos n \theta_{1}+i \sin n \theta_{1}\right) $$
当\(r_{1}=1\)时,得\((\cos \theta_{1}+i \sin \theta_{1})^n=\cos n\theta_{1}+i \sin n\theta_{1}\),这个公式叫做德·莫弗公式.
$$ z_{1}^{\frac{1}{n}}=r_{1}^{\frac{1}{n}}\left(\cos \frac{\theta_{1}+2 k \pi}{n}+i \sin \frac{\theta_{1}+2 k \pi}{n}\right) \quad(k=0,1,2, \cdots, n-1) $$
[指数式运算] 设
$$ z_{1}=r_{1} e^{i \theta_{1}} \quad z_{2}=r_{2} e^{i \theta_{2}} $$
则
$$ z_{1} \cdot z_{2}=r_{1} r_{2} e^{i\left(\theta_{1}+\theta_{2}\right)} \quad \frac{z_{1}}{z_{2}}=\frac{r_{1}}{r_{2}} e^{i\left(\theta_{1}-\theta_{2}\right)} $$
$$ z^{n}=r^{n} e^{i n \theta} \quad z^{\frac{1}{n}}=r^{\frac{1}{n}} e^{i \frac{\theta+2 k \pi}{n}} \quad(k=0,1,2, \cdots, n-1) $$
三、数列与简单级数
1.数列与级数的概念
依照某种规则排列着的一列数
$$ a_{1}, a_{2}, a_{3}, \cdots, a_{n}, \cdots $$
称为数列,记作{\(a_{n}\)}. 若把这一列数用和号联接起来:
$$ a_{1}+a_{2}+a_{3}+\cdots+a_{n}+\cdots $$
它称为级数,记作 \(\sum_{n=1}^{\infty} a_{n}\). \(a_{n}\) 称为该数列或相应级数的通项(或称为一般项).
2.等差数列与等差(算术)级数
$$ a_{1}, a_{1}+d, a_{1}+2 d, a_{1}+3 d, \cdots \quad(d \text { 为常数 }) $$
称为公差为\(d\)的等差数列. 与等差数列相应的级数称为等差级数,又称算术级数.
通项公式 \(a_{n}=a_{1}+(n-1)d\)
前 n 项和 \(S_{h}=\frac{\left(a_{1}+a_{n}\right) n}{2}=n a_{1}+\frac{n(n-1)}{2} d\)
等差中项 \(a_{k}=\frac{a_{k-1}+a_{k+1}}{2} \quad(k>1)\)
3.等比数列与等比(几何)级数
$$ a_{1}, a_{1} q, a_{1} q^{2}, a_{1} q^{3}, \cdots \quad(q \text { 为常数 }) $$
称为公比为 q 的等比数列.与等比数列相应的级数称为等比级数,又称几何级数.
通项公式 \(a_{n}=a_{1} q^{n-1}\)
前 n 项和 \(S_{n}=\frac{a_{1}\left(1-q^{n}\right)}{1-q}=\frac{a_{1}-a_{n} q}{1-q}\)
等比中项 \(a_{k}=\pm \sqrt{a_{k-1} a_{k+1}} \quad\left(a_{k-1} a_{k+1}>0\right)\)
无穷递减等比级数的和 \(S=\sum_{n=1}^{\infty} a_{1} q^{n-1}=\frac{a_{1}}{1-q} \quad(|q|<1)\)
4.算术-几何级数
$$ \sum_{k=0}^{n-1}(a+k d) q^{k}=\frac{a-[a+(n-1) d] q^{n}}{1-q}+\frac{d q\left(1-q^{n-1}\right)}{(1-q)^{2}} \quad(n \mid \geqslant 1) $$
$$ \sum_{k=0}^{\infty}(a+k d) q^{k}=\frac{a}{1-a}+\frac{d q}{(1-a)^{2}} \quad(|q|<1) $$
5.调和级数
1° 若 \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\cdots\) 为等差级数,则 \(a+b+c+\cdots\) 称为调和级数. 调和中项为
$$ b=\frac{2 a c}{a+c} $$
2° 设A, G, H分别为某两个数的等差中项、等比中项和调和中项,则
$$ A H=G^{2} $$
6.高阶等差级数
设有一数列
$$ a1, a2, \cdots, an, \cdots \qquad \qquad \qquad \qquad \qquad \quad (1) $$
如果接连地从它的后一项减去前一项,那末就得到原数列(1)的第一次差构成的数列
$$ a_{2}-a_{1}, a_{3}-a_{2}, \cdots, a_{n}-a_{n-1}, \cdots \qquad \qquad (2) $$
再接连地将(2)的后一项减去前一项,又得到数列(1)的第二次差构成的数列.依次类推:
$$ \begin{array}{lccccccc} & a_{1} & & a_{2} & & a_{3} & & a_{4} & \\ \text { 第一次差 } & & d_{1}=\Delta a_{1} & & \Delta a_{2} & & \Delta a_{3} & & \ldots \\ \text { 第二次差 } & & & d_{2}=\Delta^{2} a_{1} & & \Delta^{2} a_{2} & & \ldots & \\ \text { 第三次差 } & & & & d_{3}=\Delta^{3} a_{1} & & \ldots & & \\ \text { } & & & & & \ldots & & & \end{array} $$
式中 \(\Delta^{k} a_{i}=\Delta^{k-1} a_{i+1}-\Delta^{k-1} a_{i}\)
如果做了 r 次,数列(1)的每个第 r 次差都相等,那末以后各次差都等于零,则称数列(1)为 r 阶等差数列. 与这样的数列相应的级数称为 r 阶等差级数. 一阶等差级数也就是通常的算术级数.
设(1)是 r 阶等差数列,并设\(d_{1}\)为(1)的第一次差构成的数列的首项,\(d_{2}\)为(1)的第二次差构成的数列的首项,\(\cdots , d_{r}\)为(1)的第 r 次差构成的数列的首项,则有
通项公式 (n>r)
$$ a_{n}=a_{1}+(n-1) d_{1}+\frac{(n-1)(n-2)}{2 !} d_{2}+\cdots+\frac{(n-1)(n-2) \cdots(n-r)}{r !} d_{r} $$
前 n 项和
$$ S_{n}=n a_{1}+\frac{n(n-1)}{2 !} d_{1}+\frac{n(n-1)(n-2)}{3 !} d_{2}+\cdots+\frac{n(n-1)(n-2) \cdots(n-r)}{(r+1) !} d_{r} $$
7.某些级数的部分和
四、乘法与因式分解公式
五、分式
1.分式运算
$$ \begin{array}{ll} \frac{a}{b} \pm \frac{c}{b}=\frac{a \pm c}{b} & \frac{a}{b}+\frac{c}{d}=\frac{a d \pm b c}{b d} \\ \frac{a}{b} \cdot \frac{c}{d}=\frac{a c}{b d} & \frac{a}{b} \div \frac{c}{d}=\frac{a d}{b c} \\ \left(\frac{a}{b}\right)^{n}=\frac{a^{n}}{b^{n}} & \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}(a>0, b>0) \end{array} $$
2.部分分式
任一既约真分式(分子与分母没有公因子,分子次数低于分母次数)都可唯一地分解成形如 \(\frac{A}{(x-a)^{k}} \text { 或 } \frac{a x+b}{\left(x^{2}+p x+q\right)^{l}}\left(\text { 其中 } \frac{p^{2}}{4}-q<0\right)\) 的基本真分式之和,其运算称为部分分式展开. 若为假分式(分子次数不低于分母次数),应先化为整式与真分式之和,然后再对真分式进行部分分式展开. 部分分式的各个系数可以通过待定系数法来确定. 下面分几种不同情况介绍.
设
$$ N(x)=n_{0}+n_{1} x+n_{2} x^{2}+\cdots+n_{r} x^{r} $$
$$ G(x)=g_{0}+g_{1} x+g_{2} x^{2}+\cdots+g_{s} x^{s} $$
[线性因子重复]
1° \(\frac{N(x)}{(x-a)^{m}}=\frac{A_{0}}{(x-a)^{m}}+\frac{A_{1}}{(x-a)^{m-1}}+\cdots+\frac{A_{m-1}}{x-a}\)
式中\(N_{x}\)的最高次数 r≤m-1;\(A_{0}\),\(A_{1}\),...,\(A_{m-1}\) 为待定常数,可由下式确定:
2° \(\frac{N(x)}{x^{m} G(x)}=\frac{A_{0}}{x^{m}}+\frac{A_{1}}{x^{m-1}}+\cdots+\frac{A_{m-1}}{x}+\frac{F(x)}{G(x)}\)
式中(A_{0}\),\(A_{1}\),...,\(A_{m}\)为待定常数,可由下式确定:
$$ \begin{aligned} &A_{0}=\frac{n_{0}}{g_{0}}, \quad A_{j}=\frac{1}{g_{0}}\left(n_{j}-\sum_{i=0}^{j-1} A_{i} g_{j-i}\right) \quad(j=1,2, \cdots, m-1) \\ &F(x)=f_{0}+f_{1} x+f_{2} x^{2}+\cdots+f_{k} x^{k}, k \leqslant s-1 \end{aligned} $$
其系数\(f_{j}\)与 m 有关,由下表确定:
例
$$ \frac{x^{2}+1}{x^{3}\left(x^{2}-3 x+6\right)}=\frac{A_{0}}{x^{3}}+\frac{A_{1}}{x^{2}}+\frac{A_{2}}{x}+\frac{f_{1} x+f_{0}}{x^{2}-3 x+6} $$
解 依上述公式算出
$$ \begin{aligned} &A_{0}=\frac{n_{0}}{g_{0}}=\frac{1}{6} \quad A_{1}=\frac{1}{g_{0}}\left(n_{1}-A_{0} g_{1}\right)=\frac{1}{6}\left[0-\frac{1}{6} \times(-3)\right]=\frac{1}{12} \\ &A_{2}=\frac{1}{g_{0}}\left(n_{2}-A_{0} g_{2}-A_{1} g_{1}\right)=\frac{1}{6}\left[1-\frac{1}{6} \times 1-\frac{1}{12} \times(-3)\right]=\frac{13}{72} \end{aligned} $$
此时 m=3,
$$ \begin{aligned} &f_{0}=n_{3}-\left(A_{0} g_{3}+A_{1} g_{2}+A_{2} g_{1}\right)=0-\left[\frac{1}{6} \times 0+\frac{1}{12} \times 1+\frac{13}{72} \times(-3)\right]=\frac{33}{72} \\ &f_{1}=n_{4}-\left(A_{0} g_{4}+A_{1} g_{3}+A_{2} g_{2}\right)=0-\left(0+0+\frac{13}{72} \times 1\right)=-\frac{13}{72} \end{aligned} $$
所以得到
$$ \frac{x^{2}+1}{x^{3}\left(x^{2}-3 x+6\right)}=\frac{1}{6 x^{3}}+\frac{1}{12 x^{2}}+\frac{13}{72 x}+\frac{-13 x+33}{72\left(x^{2}-3 x+6\right)} $$
3° \(\frac{N(x)}{(x-a)^{m} G(x)}=\frac{A_{0}}{(x-a)^{m}}+\frac{A_{1}}{(x-a)^{m-1}}+\frac{A_{2}}{(x-a)^{m-2}}+\cdots+\frac{A_{m-1}}{x-a}+\frac{F(x)}{G(x)}\)
作变换 \(y=x-a\), 则 \(N(x)=N_{1}(y), G(x)=G_{1}(y)\), 上式变为 $$ \frac{N_{1}(y)}{y^{m} G_{1}(y)}=\frac{A_{0}}{y^{m}}+\frac{A_{1}}{y^{m-1}}+\frac{A_{2}}{y^{m-2}}+\cdots+\frac{A_{m-1}}{y}+\frac{F_{1}(y)}{G_{1}(y)} $$
用上述1°,2°的方法确定出\(A_{0}, A_{1}, \cdots, A_{m-1}\)和\(F_{1}(y)\),再将\(y=x-a\)代回. 也可按下式来确定系数\(A_{0}, A_{1}, \cdots, A_{m-1}\):
$$ A_{k}=\frac{1}{k !}\left[\frac{d^{k}}{d x^{k}}\left(\frac{N(x)}{G(x)}\right)\right]_{x-a} \quad(k=0,1,2, \cdots, m-1) $$
[线性因子不重复]
1° \(\frac{N(x)}{(x-a)(x-b)(x-c)}=\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\)
式中N(x)的最高次数r≤2,a≠b≠c;A, B, C为待定常数,可由下式确定:
2° \(\frac{N(x)}{(x-a)(x-b) G(x)} =\frac{A}{x-a}+\frac{B}{x-b}+\frac{F(x)}{G(x)} \quad(a \neq b) \)
式中多项式\(F(x)\)的最高次数k≤s-1;A, B为待定常数,用下式确定:
A, B确定后,再用等式两边多项式同次项系数必须相等的法则来确定\(F(x)\)的各项系数.
例 \(\frac{x^{2}+3}{x(x-2)\left(x^{2}+2 x+4\right)}=\frac{A}{x}+\frac{B}{x-2}+\frac{f_{1} x+f_{0}}{x^{2}+2 x+4}\)
解 依上述公式算得
把A,B代入原式,通分并整理后得
$$ x^{2}+3=\left(f_{1}-\frac{3}{8}+\frac{7}{24}\right) x^{3}+\left(f_{0}-2 f_{1}+\frac{7}{12}\right) x^{2}+\left(\frac{7}{6}-2 f_{0}\right) x+3 $$
比较等式两边同次项系数得
$$ f_{0}=\frac{7}{12} \quad f_{1}=\frac{1}{12} $$
所以有
$$ \frac{x^{2}+3}{x(x-2)\left(x^{2}+2 x+4\right)}=-\frac{3}{8 x}+\frac{7}{24(x-2)}+\frac{x+7}{12\left(x^{2}+2 x+4\right)} $$
[高次因子]
$$ \begin{aligned} &\frac{N(x)}{\left(x^{2}+h_{1} x+h_{0}\right) G(x)}=\frac{a_{1} x+a_{0}}{x^{2}+h_{1} x+h_{0}}+\frac{F(x)}{G(x)} \\ &\frac{N(x)}{\left(x^{2}+h_{1} x+h_{0}\right)^{2} G(x)}=\frac{a_{1} x+a_{0}}{\left(x^{2}+h_{1} x+h_{0}\right)^{2}}+\frac{b_{1} x+b_{0}}{x^{2}+h_{1} x+h_{0}}+\frac{F(x)}{G(x)} \\ &\frac{N(x)}{\left(x^{3}+h_{2} x^{2}+h_{1} x+h_{0}\right) G(x)}=\frac{a_{2} x^{2}+a_{1} x+a_{0}}{x^{3}+h_{2} x^{2}+h_{1} x+h_{0}}+\frac{F(x)}{G(x)} \end{aligned} $$
[计算系数的一般方法]
$$ \frac{N(x)}{D(x)}=\frac{N(x)}{G(x) H(x) L(x)}=\frac{A(x)}{G(x)}+\frac{B(x)}{H(x)}+\frac{C(x)}{L(x)}+\cdots $$
1° 等式两边乘以\(D(x)\)化为整式,各项按x的同次幂合并,然后列出未知系数的方程组,解出而得.
2° 等式两边乘以\(D(x)\)化为整式,再把x用简单的数值(如x=0, 1, -1等)代入,然后列出未知系数的方程组,解出而得.
六、比例
1° 若 \(\frac{a}{b}=\frac{c}{d}\) (或写为a:b=c:d),a, b, c, d 都不等于零,则
$$ \begin{aligned} &a d=b c \quad \text { (交叉积) } \quad\frac{b}{a}=\frac{d}{c} \text { (反比) } \\ &\frac{a}{c}=\frac{b}{d} \quad \text { (更比) } \quad \frac{a+b}{b}=\frac{c+d}{d} \text { (合比) }\\ &\frac{a-b}{b}=\frac{c-d}{d} \quad \text { (分比) } \quad \frac{a+b}{a-b}=\frac{c+d}{c-d} \text { (合分比)) } \end{aligned} $$
2° 若 \(\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\cdots=\frac{a_{n}}{b_{n}}\), 则
$$ \frac{a_{1}}{b_{1}}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{b_{1}+b_{2}+\cdots+b_{n}}=\frac{\lambda_{1} a_{1}+\lambda_{2} a_{2}+\cdots+\lambda_{n} a_{n}}{\lambda_{1} b_{1}+\lambda_{2} b_{2}+\cdots+\lambda_{n} b_{n}}=\frac{\sqrt{a_{1}^{2}+a_{2}^{2}+\cdots+a_{n}^{2}}}{\sqrt{b_{1}^{2}+b_{2}^{2}+\cdots+b_{n}^{2}}} $$
式中\(λ_{i}(i=1, 2, \cdots, n)\)为一组任意的常数,\(b_{i}(i=1, 2, \cdots, n)\)都不等于零.
3° 若 y 与 x 成正比,(记作y∝x),则
$$ y=kx \quad k \text {为比例常数} $$
若 y 与 x 成反比 \(\left(\text { 记作 } y \propto \frac{1}{x}\right)\),则
$$ y = \frac{k}{x} \quad k \text{为比例常数} $$
若 y 与 x 成正比,y 与 z 也成正比(即y∝x, y∝z),则x与z成正比,即
$$ x=kz \quad (x∝z) $$
且y与xz成正比,即
$$ x=kxz \quad (x∝xz) $$
七、根式
1.根式的概念
[方根与根式] 数a的n次方根是指求一个数,它的 n 次方恰好等于 a. a 的 n 次方根记为 \(\sqrt[n]{a}\) (n 为大于 1 的自然数). 作为代数式,\(\sqrt[n]{a}\) 称为根式. n称为根指数,a 称为根底数. 在实数范围内,负数不能开偶次方,一个正数开偶次方有两个方根,其绝对值相同,符号相反.
[算术根] 正数的正方根称为算术根.零的算术根规定为零.
[基本性质] 由方根的定义,有
$$ (\sqrt[n]{a})^{n}=a=\sqrt[n]{a^{n}} $$
2.根式运算
[乘积的方根] 乘积的方根等于各因子同次方根的乘积;反过来,同次方根的乘积等于乘积的同次方根,即
$$ \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}(a \geqslant 0, b>0) $$
[根式的乘方] \((\sqrt[n]{a})^{m}=\sqrt[n]{a^{m}}(a \geqslant 0)\)
[根式化简]
[同类根式及其加减运算] 根指数和根底数都相同的根式称为同类根式,只有同类根式才可用加减运算加以合并.
八、不等式
1.简单不等式
1° 若a>b,则
$$ \begin{array}{ll} a \pm c>b \pm c & c-a<c-b \\ a c>b c & \frac{a}{c}>\frac{b}{c}(c>0) \\ a c<b c & \frac{a}{c}<\frac{b}{c}(c<0) \\ a^{n}>b^{n} & (n>0, a>0, b>0) \\ a^{n}<b^{n} & (n<0, a>0, b>0) \\ \sqrt[n]{a}>\sqrt[n]{b} & (n \text { 为正整数, } a>0, b>0) \end{array} $$
2° 若 \(\frac{a}{b}=\frac{c}{d}\) ,且b、d同号,则
$$ \frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d} $$
2. 有关绝对值的不等式
1° 若a, b, ..., k为任意复数,则
$$ \begin{aligned} &|a \pm b| \leqslant|a|+|b| \\ &|a \pm b \pm \cdots \pm k| \leqslant|a|+|b|+\cdots+|k| \end{aligned} $$
2° 若a, b为任意复数,则
$$ |a|-|b| \leqslant|a-b| \leqslant|a|+|b| $$
3° 若\(|a| \le b, b>0\),则
$$ -b \leqslant a \leqslant b \text { 特别有 }-|a| \leqslant a \leqslant|a| $$
4° 若\(|a| \ge b, b>0\),则
$$ a>b 或 a<-b $$
3.有关三角函数、指数函数、对数函数的不等式
\(\sin x<x<\tan x \quad\left(0<x<\frac{\pi}{2}\right)\)
\(\cos x<\frac{\sin x}{x}<1 \quad(0<x<\pi)\)
\(\frac{\sin x}{x}>\frac{2}{\pi} \quad\left(-\frac{\pi}{2}<x<\frac{\pi}{2}\right)\)
\(\cos x>1-\frac{1}{2} x^{2} \quad(-\infty<x<\infty, x \neq 0)\)
\(\sin x>x-\frac{1}{6} x^{3}\)
\((x>0)\)
\(\tan x>x+\frac{1}{3} x^{3}\)
\(\left(0<x<\frac{\pi}{2}\right)\)
\(\pi<\frac{\sin \pi x}{x(1-x)}<4 \quad\left(0<x<1, x \neq \frac{1}{2}\right)\)
\((x \neq 0)\)
\(e^{x}<\frac{1}{1-x}\)
\((x<1, x \neq 0)\)
\(e^{x}>1+x+\frac{x^{2}}{2 !}+\cdots+\frac{x^{n}}{n !} \quad(n$ 为自然数, $x>0)\)
\((x \neq 0)\)
\(\frac{x}{1+x}<1-e^{-x}\)
\((x>-1, x \neq 0)\)
\(e^{\frac{x}{1+x}}<1+x\)
\((x>-1, x \neq 0)\)
\(\frac{x}{1+x}<\ln (1+x)<x\)
\((x>-1, x \neq 0)\)
特别取 \(x=\frac{1}{n}\) ( n 为自然数), 有
$$ \begin{array}{c} \frac{1}{n+1}<\ln \left(1+\frac{1}{n}\right) <\frac{1}{n} \\ \ln x \leq x-1 (x>0) \ x<-\ln (1-x)<\frac{x}{1-x} (x<1, x \neq 0) \\ \ln x \leq n\left(x^{\frac{1}{n}}-1\right) (n>0, x>0) \\ \ln \sec x<\frac{1}{2} \sin x \cdot \tan x \left(0<x<\frac{1}{2}\right) \\ (1+x)^{a}>1+x^{\alpha} (\alpha>1, x>0) \end{array} $$
(以下各式变数 $z$ 为复数)
\(|\cos z|<2 \quad(|z|<1)\)
\(|\sin z|<\frac{6}{5}|z| \quad(0<|z|<1)\)
\(\left|e^{z}-1\right|<e^{|t|-1}<|z| e^{|\neq|} \quad(z \neq 0)\)
\(\frac{1}{4}|z|<\left|e^{z}-1\right|<\frac{7}{4}|z| \quad(0<|z|<1)\)
\(|\ln (1+z)|<-\ln (1-|z|) \quad(0<|z|<1)\)
4.某些重要不等式
[算术平均值与几何平均值不等式]
1° 几个数的算术平均值的绝对值不超过这些数的均方根,即
$$ \left|\frac{a_{1}+a_{2}+\cdots+a_{n}}{n}\right| \leq \sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\cdots+a_{n}^{2}}{n}} $$
等号只当\(a_{1}=a_{2}=\cdots=a_{n}\)时成立.
2° 设\(a_{1}, a_{2}, \cdots, a_{n}\)均为正数,则它们的几何平均值不超过算术平均值,即
$$ \sqrt[n]{a_{1} a_{2} \cdots a_{n}} \leq \frac{a_{1}+a_{2}+\cdots+a_{n}}{n} $$
3° 对 n 个正数\(a_{1}, a_{2}, \cdots, a_{n}\)的加权平均值\(\frac{p_{1} a_{1}+p_{2} a_{2}+\cdots+p_{n} a_{n}}{p_{1}+p_{2}+\cdots+p_{n}}\),有
$$ a_{1}^{p_{1}} a_{2}^{p_{2}} \cdots a_{n}^{p_{n}} \leq\left(\frac{p_{1} a_{1}+p_{2} a_{2}+\cdots+p_{n} a_{n}}{p_{1}+p_{2}+\cdots+p_{n}}\right)^{p_{1}+p_{2}+\cdots+p_{n}} $$
4° 设\(a_{1}, a_{2}, \cdots, a_{n}\)为正数,又\(α<0<β\),则有
$$ \left(\frac{1}{n} \sum_{i=1}^{n} a_{i}^{a}\right)^{\frac{1}{\alpha}} \leq\left(a_{1} a_{2} \cdots a_{n}\right)^{\frac{1}{n}} \leq\left(\frac{1}{n} \sum_{i=1}^{n} a_{i}^{\beta}\right)^{\frac{1}{\beta}} $$
[柯西不等式] 设\(a_{i}, b_{i}(i=1, 2, \cdots, n)\)为任意实数,则
$$ \left(\sum_{i=1}^{n} a_{i} b_{i}\right)^{2} \leq\left(\sum_{i=1}^{n} a_{i}^{2}\right)\left(\sum_{i=1}^{n} b_{i}^{2}\right) $$
等号只当\(\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\cdots=\frac{a_{n}}{b_{n}}\)时成立. 这个不等式表明一个角(取实数值)的余弦值总是小于 1 的,或者说二矢量内积小于二矢量长度之积.
[赫尔德不等式]
1° 设\(a_{i}, b_{i}, \cdots, l_{i}(i=1, 2, \cdots, n)\)为正数,又\(α, β, \cdots, λ\)为正数,且 \(α+β+\cdots+λ=1\),则
$$ \sum_{i=1}^{n} a_{i}^{a} b_{i}^{\beta} \cdots l_{l}^{\lambda} \leq\left(\sum_{i=1}^{n} a_{i}\right)^{a}\left(\sum_{i=1}^{n} b_{i}\right)^{\beta} \cdots\left(\sum_{i=1}^{n} l_{i}\right)^{2} $$
等号只当 \(\frac{a_{k}}{\sum a_{i}}=\frac{b_{k}}{\sum b_{i}}=\cdots=\frac{l_{k}}{\sum l_{s}}\) 时成立.
2° 设\(a_{i}, b_{i} (i=1, 2, \cdots, n)\)为正数,又 k>0, k≠1, ′k与k共轭,即 \(\frac{1}{k'}+\frac{1}{k}=1\),或 \((k-1)(k'-1)=1\),则
$$ \begin{aligned} &\sum_{i=1}^{n} a_{i} b_{i} \leq\left(\sum_{i=1}^{n} a_{i}^{k}\right)^{\frac{1}{k}}\left(\sum_{i=1}^{n} b_{i}^{k^{\prime}}\right)^{\frac{1}{k^{\prime}}}(k>1) \\ &\sum_{i=1}^{n} a_{i} b_{i} \geq\left(\sum_{i=1}^{n} a_{i}^{k}\right)^{\frac{1}{k}}\left(\sum_{i=1}^{n} b_{i}^{k^{\prime}}\right)^{\frac{1}{k^{\prime}}}(k<1) \end{aligned} $$
等号只当 \(\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\cdots=\frac{a_{n}}{b_{n}}\) 时成立.
[闵可夫斯基不等式] 设\(a_{i}, b_{i}>0 (i=1, 2, \cdots, n)\),又r>0, r≠1, 则
等号只当 \(\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\cdots=\frac{a_{n}}{b_{n}}\) 时成立. 当 r=2 时,此不等式也称为三角形不等式,它表明三角形两边之和大于第三边.
[契贝谢夫不等式] 设\(a_{i}>0, b_{i}>0 (i=1, 2, \cdots, n)\).若\(a_{1} \le a_{2} \le \cdots \le a_{n}\), 且\(b_{1} \le b_{2} \le \cdots \le b_{n}\), 或 \(a_{1} \ge a_{2} \ge \cdots \ge a_{n}\), 且 \(b_{1} \ge b_{2} \ge \cdots \ge b_{n}\), 则
$$ \left(\frac{1}{n} \sum_{i=1}^{n} a_{i}\right)\left(\frac{1}{n} \sum_{i=1}^{n} b_{i}\right) \leq \frac{1}{n} \sum_{i=1}^{n} a_{i} b_{i} $$
若\(a_{1} \le a_{2} \le \cdots \le a_{n}\) 而\(b_{1} \ge b_{2} \ge \cdots \ge b_{n}\),则
$$ \left(\frac{1}{n} \sum_{i=1}^{n} a_{i}\right)\left(\frac{1}{n} \sum_{i=1}^{n} b_{i}\right) \geq \frac{1}{n} \sum_{i=1}^{n} a_{i} b_{i} $$
[詹生不等式] 设\(a_{i}>0 (i=1, 2, \cdots, n)\),且 0<r≤s,则
$$ \left(\sum_{i=1}^{n} a_{i}^{s}\right)^{\frac{1}{s}} \leq\left(\sum_{i=1}^{n} a_{i}^{r}\right)^{\frac{1}{r}} $$
[伯努利不等式] 设a>1,自然数n>1,则
$$ a^{n}>1+n(a-1) $$
特别令 \(a=b^{\frac{1}{n}}(b>1)\) ,则
$$ b^{\frac{1}{n}}-1<\frac{b-1}{n} $$
5.二次不等式解法
九、阶乘、排列与组合
1. 阶乘
[阶乘的定义] 设 n 为自然数,则
$$ n!=1·2·3 \cdots n $$
称为 n 的阶乘. 并且规定\(0!=1\). 又定义
$$ (2n+1)!!=\frac{(2n+1)!}{2^nn!}=1·3·5 \cdots (2n+1), (-1)!!=0 $$
$$ (2n)!!=2^nn!=2·4·6 \cdots (2n), 0!!=0 $$
[斯特林公式]
$$ \begin{aligned} &n !=\sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n} e^{\frac{\theta}{12 n}}(0<\theta<1) \\ &n ! \approx \sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}(\text { 当 } n \text { 充分大 }) \\ &\sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}<n !<\sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}\left(1+\frac{1}{12 n-1}\right) \end{aligned} $$
[阶乘有限和公式]
$$ \begin{aligned} &\sum_{j=1}^{n} j ! j=(n+1) !-1 \\ &\sum_{j=1}^{n} \frac{j}{(j+1) !}=1-\frac{1}{(n+1) !} \\ &\sum_{j=1}^{n} \frac{j^{2}+j-1}{(j+2) !}=\frac{1}{2}-\frac{n+1}{(n+2) !} \\ &\sum_{j=1}^{n} \frac{j 2^{j}}{(j+2) !}=1-\frac{2^{n+1}}{(n+2) !} \\ &\sum_{j=0}^{n} \frac{1}{j !(n-j) !}=\frac{2^{n}}{n !} \\ &\sum_{j=0}^{n}(-1)^{j} \frac{n(n+j-1) !}{(j !)^{2}(n-j) !}=0 \\ &\sum_{j=1}^{n} \frac{j}{(2 j+1) ! !}=\frac{1}{2}\left[1-\frac{1}{(2 n+1) ! !}\right] \\ &\sum_{j=1}^{n} \frac{(2 j-1) ! !}{(2 j+2) ! !}=\frac{1}{2}-\frac{(2 n+1) ! !}{(2 n+2) ! !} \end{aligned} $$
2. 排列
[选排列] 从 n 个不同的元素中,每次取出 k 个(k≤n)不同的元素,按一定的顺序排成一列,称为选排列. 其排列种数为
$$ A^k_{n}=n(n-1)(n-2)\cdots(n-k+1)=\frac{n!}{(n-k)!} $$
[全排列] 从 n 个不同的元素中,每次取出 n 个不同的元素,按一定的顺序排成一列,称为全排列.其排列种数为
$$ P_{n}=A^n_{n}=n(n-1)(n-2)\cdots3·2·1=n! $$
[有重复的排列] 从 n 个不同的元素中,每次取出 k 个元素(k≤n),允许重复,这种排列称为有重复的排列.其排列种数为
$$ A_{n}^\tilde{k}=n^k \qquad A_{n}^\tilde{n}=n^n $$
[不尽相异元素的全排列] 如果在 n 个元素中,有\(n_{1}\) 个元素彼此相同,又有\(n_{2}\)个元素彼此相同,...,又有\(n_{m}\)个元素彼此相同\(n_{1}+n_{2}+\cdots+n_{m}=n)\),那末这 n 个元素的全排列称为不尽相异元素的全排列. 其排列种数为
$$ A^n_{\tilde{n}(n_{1},n_{2},\cdots,n_{m})}=\frac{n!}{n_{1}!n_{2}! \cdots n_{m}!} $$
[环状排列] 从 n 个不同元素中,每次取出 k 个元素,仅按元素之间的相对位置而不分首尾地围成一圈,这种排列法称为环状排列. 其排列种数为
$$ A^ⓚ_{n}=\frac{A^k_{n}}{k} $$
3. 组合
[通常意义下的组合] 从 n 个不同的元素中,每次取出 k 个不同的元素,不管其顺序合并成一组,称为组合. 其组合种数为
$$ C_{n}^{k}=\frac{A_{n}^{k}}{k !}=\frac{n !}{(n-k) ! k !}\left(C_{n}^{k} \text { 也记作 }\left(\begin{array}{l} n \\ k \end{array}\right)\right) $$
并且规定 \(C^0_{n}=1\).
[多组组合] 把 n 个不同的元素分成 m 组,第 i 组有\(n_{i}\)个不同的元素,即\(n_{1}+n_{2}+\cdots+n_{m}=n\),这样分组的种数为
$$ C_{n}^{k}=\frac{A_{n}^{k}}{k !}=\frac{n !}{(n-k) ! k !}\left(C_{n}^{k} \text { 也记作 }\left(\begin{array}{l} n \\ k \end{array}\right)\right) $$
通常意义下的组合是其特例.
[有重复的组合] 从 n 个不同元素中,每次取出 k 个元素,允许重复,不管其顺序合并成一组,这种组合称为有重复的组合,其组合种数为
$$ C_{n}^{\tilde{k}}=C_{n+k-1}^{k} $$
[组合公式]
十、杨辉三角形与多项式定理
[二项式定理]
$$ \begin{aligned} (a+b)^{n} &=C_{n}^{0} a^{n}+C_{n}^{1} a^{n-1} b+C_{n}^{2} a^{n-2} b^{2}+\cdots+C_{n}^{n-1} a b^{n-1}+C_{n}^{n} b^{n} \\ &=\sum_{k=0}^{n} C_{n}^{k} a^{n-k} b^{k} \end{aligned} $$
式中 n 为正整数,\(C^k_{n}\)称为二项系数.
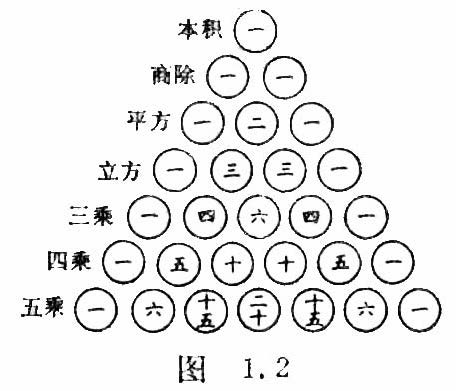
[杨辉三角形] 我国南宋时期数学家杨辉在他所著的《详解九章算法》(1261年)中记载着有关二项系数的研究.在二项式定理中,当n分别取0, 1, 2, 3, 4, 5, 6时,其二项系数表示成图1.2,即所谓“杨辉三角形”. 法国人帕斯卡也有类似结果(1650年),故外国书刊中称之为“帕斯卡三角形”,但比杨辉晚了近四百年.
[多项式定理]
\((a+b+\cdots+f)^{n}=\sum_{p+q+\cdots+s=n} \frac{n !}{p ! q ! \cdots s !} a^{p} b^{q} \cdots f^{s}\) 和式中每一数组(p, q, ..., s)对应一项,这个数组满足0≤p≤n, 0≤q≤n, ..., 0≤s≤n, p+q+...+s=n, Σ是对于所有这样的数组求和.
十一、数学归纳法与抽屉原理
[数学归纳法] 对于包含整数 n 的公式,即从某一整数起对后面所有整数 n 都成立的公式,有时可用数学归纳法来证明.其步骤如下:
1° 验证 n 取第一个值\(n_{0}\) 时(如\(n_{0}=0, 1或2等\))公式成立.
2° 假定当 n=k 时公式成立,验证当 n=k+1 时公式也成立.
因为公式当\(n=n_{0}\)时成立,所以由2°可知,当\(n=n_{0}+1\)时公式也成立;再由2°可知,当\(n=n_{0}+1+1=n_{0}+2\)时公式也成立,如此继续推下去可知,对一切大于\(n_{0}\)的整数 n 公式都成立.
[抽屉原理] n+1 个物体放入 n 个抽屉里,至少有一个抽屉有两个以上的物体,这个原理称为抽屉原理,它在证明某些存在性定理时很有用. 抽屉原理分以下三种形式:
1° n+1 个元素分成 n 组,必有一组至少包含两个元素.
2° m 个元素分成 n 组(m>n为正整数),必有一组至少包含\(\left[\frac{m-1}{n}\right]+1\)个元素([x]表示x的整数部分).
3° 无限多个元素分成有限组,必有一组包含无限多个元素.
§2 初等函数及其数值计算
一、函数的概念与分类
[函数与反函数] 设 D 是给定的一个数集. 若有两个变量 x 和 y,当变量 x 在 D 中取某个特定值时,变量 y 依确定的关系f也有一个确定的值,则称 y 是 x 的函数,f 称为 D 上的一个函数关系,记为 y=f(x),x 称为自变量,y 称为因变量. 当 x 取遍 D 中各数,对应的 y 构成一数集 R,D 称为定义域或自变数域,R 称为值域或因变数域. 反过来,若把 y 视为自变量,x 视为因变量,用 y 写出 x 的表达式:\(x=ϕ(y)\),则称 \(y=f(x)\) 与 \(x=ϕ(y)\) 互为反函数.
[实变函数与复变函数] 当自变数域为实数域时,函数称为实变函数.当自变数域为复数域时,函数称为复变函数.
[一元函数与多元函数] 只有一个自变量的函数称为一元函数.有两个或两个以上自变量的函数称为多元函数.
[显函数与隐函数] 因变量可以由自变量用数学式子直接表示出来的函数称为显函数. 若函数关系包含在一个方程式或一组方程式中,自变量与因变量无明显区分,则称为隐函数.
[简单函数与复合函数] 若 y 是 u 的函数 \(y=f(u)\),而 u 又是 x 的函数,\(u=ϕ(x)\),则 y 称为 x 的复合函数,u 称为中间变量,记作 \(y=f[ϕ(x)]\),无中间变量的函数称为简单函数.
[有界函数与无界函数] 若存在两个数 m, M(m≤M),使 m≤f(x)≤M ,对定义域上的任意x都成立,则称 f(x) 为定义域上的有界函数,m 为其下界,M 为其上界. 若这样的数m和M至少有一个不存在,则称 f(x) 为定义域上的无界函数.
[单调函数与非单调函数] 若对于区间[a, b]中的任意 \(x_{1}>x_{2}\)有 \(f(x_{1})≥f(x_{2})\) [或\(f(x_{1})≤f(x_{2})\)],则称f(x)为[a, b]中的递增函数(或递减函数).递增函数和递减函数通称为单调函数.不是递增(或递减)的函数称为非单调函数.
[奇函数与偶函数] 若对于定义域中的任意 x 恒有\(f(-x)=-f(x)\),则称 \(f(x)\) 为奇函数;若对于定义域中的任意 x 恒有 \(f(-x)=f(x)\),则称 \(f(x)\) 为偶函数.
[周期函数与非周期函数] 若有一实数T≠0,使对定义域中的任意 x 恒有 \(f(x+T)=f(x)\),则f(x)称为以T为周期的周期函数;否则称\(f(x)\)为非周期函数.
[单值函数与多值函数] 若对于自变量 x 的一个值,因变量 y 有一个而且只有一个值与其对应,则称 y 为 x 的单值函数. 若对于自变量 x 的一个值,与其对应的 y 值不止一个,则称 y 为 x 的多值函数.
[初等函数] 幂函数、指数函数、对数函数、三角函数、反三角函数通称为"基本初等函数",凡是由基本初等函数经过有限次四则运算以及有限次的复合步骤而构成,并能用一个数学式子表示的函数都属于初等函数.
二、幂函数与有理函数
[定义] 形如\(y=x^α\)的函数称为幂函数,式中 α 为任意实常数.
x 的多项式
$$ \begin{aligned} y=a_{0} x^{n}+a_{1} x^{n-1}+\cdots+a_{n-1} x+& a_{n} \\ &\left(a_{0}, a_{1}, \cdots, a_{n} \text { 为常数, } n\right. \text { 为自然数) } \end{aligned} $$
称为有理整函数.
两个多项式的商
$$ y=\frac{a_{0} x^{n}+a_{1} x^{n-1}+\cdots+a_{n-1} x+a_{n}}{b_{0} x^{m}+b_{1} x^{m-1}+\cdots+b_{m-1} x+b_{m}} $$
称为有理分式函数.
有理整函数和有理分式函数通称为有理函数,有时用符号\(R(x)\)表示.
[幂函数的图形与特征]
